This is very common problem that is asked in any interview. So that will be explained below:-
Before solving any recursive solution, we have to find the base case first and then the recursive portion. Here if we apply the power rule like a^(4) = a^(2) * a(^2) , then we can see one recursive pattern here. Now the base case will be a^0 or a^1, in both the case it will return 1 and the number itself, so we can easily consider a^1 as the base case.
But, what about the odd power number like, a^(5). Here also we can apply the power rule, like a^(4) * a^(1). So for the odd cases, we have to multiply with the number itself for one more time.
So, let’s check the solution in java-script. In the below mentioned code zero power value is not handled, please add this for your implementation.
//exponential recursive solution
/*******
Here the approach is if , the n is 0 or 1 , we will return the number itself, this will be the base case,
and for the logic we will use the power rule, like a^4 = a^2 * a^2
************/
function exponentialRecursive( a , n )
{
//base case define // zero value not handled intentionally
if (n ===1) {
return a;
} else if (n%2 ===0) {
// even number check
a = exponentialRecursive( a , n/2 ) * exponentialRecursive( a , n/2 );
return a;
}else if (n%2 ===1 ) {
// odd number check
a = exponentialRecursive( a , Math.floor(n/2) ) * a * exponentialRecursive( a , Math.floor(n/2) );
return a;
}
}
Illustration of the call stack:-
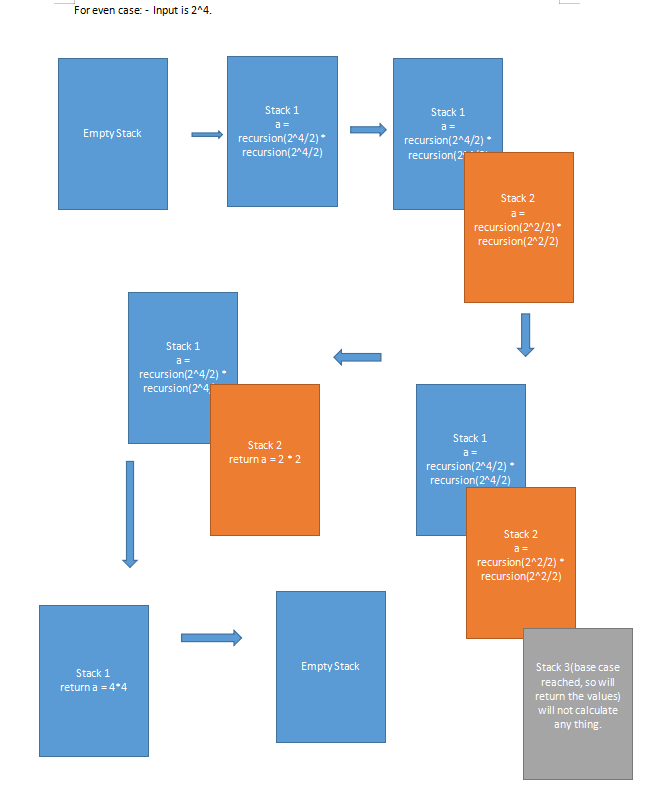
You can also check the below mentioned link, where it’s also explained with divide and conquer technique.