The product difference between two pairs (a, b) and (c, d) is defined as (a * b) – (c * d).
For example, the product difference between (5, 6) and (2, 7) is (5 * 6) - (2 * 7) = 16.Given an integer array nums, choose four distinct indices w, x, y, and z such that the product difference between pairs (nums[w], nums[x]) and (nums[y], nums[z]) is maximized. Return the maximum such product difference.
Example 1:
Input: nums = [5,6,2,7,4]
Output: 34
Explanation: We can choose indices 1 and 3 for the first pair (6, 7) and indices 2 and 4 for the second pair (2, 4).
The product difference is (6 * 7) – (2 * 4) = 34.
Example 2:
Input: nums = [4,2,5,9,7,4,8]
Output: 64
Explanation: We can choose indices 3 and 6 for the first pair (9, 8) and indices 1 and 5 for the second pair (2, 4).
The product difference is (9 * 8) – (2 * 4) = 64.
Constraints:
4 <= nums.length <= 104
1 <= nums[i] <= 104Flow Diagram: –
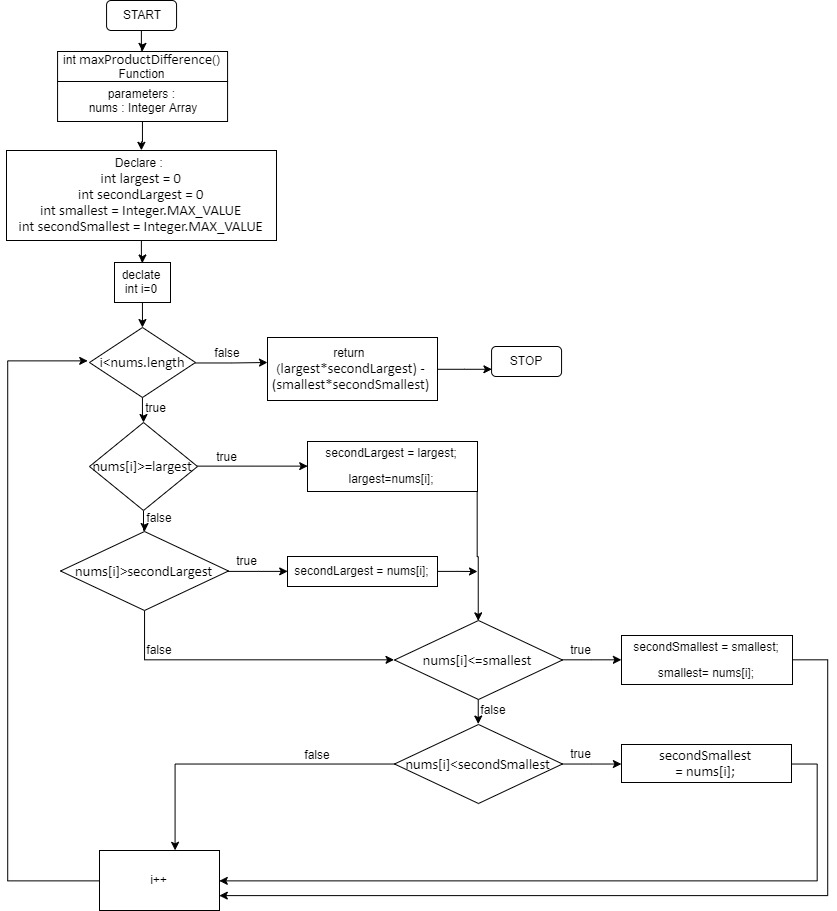
Solution: –
public int maxProductDifference(int[] nums) {
int largest = 0, secondLargest = 0, smallest = Integer.MAX_VALUE, secondSmallest = Integer.MAX_VALUE;
for(int i=0;i<nums.length;i++) {
if(nums[i]>=largest) {
secondLargest = largest;
largest = nums[i];
} else if(nums[i]>secondLargest) secondLargest = nums[i];
if(nums[i]<=smallest) {
secondSmallest = smallest;
smallest = nums[i];
} else if(nums[i]<secondSmallest) secondSmallest = nums[i];
}
return largest * secondLargest - smallest * secondSmallest;
}