Leet code problem 1926: – Nearest Exit from Entrance in Maze

You are given an m x n matrix maze (0-indexed) with empty cells (represented as ‘.’) and walls (represented as ‘+’). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.

In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit. Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.

Flow Diagram: –

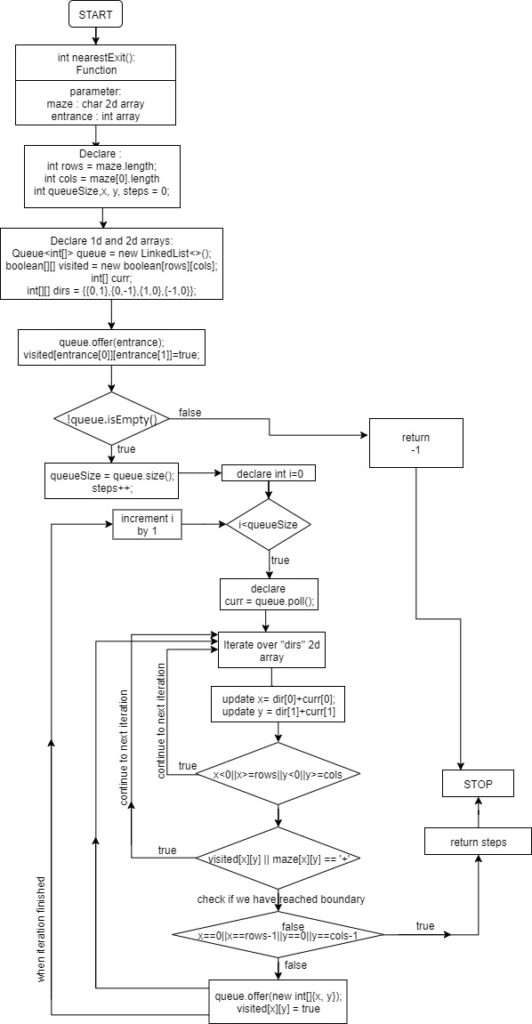
Solution: –

class Solution {
    public int nearestExit(char[][] maze, int[] entrance) {
        int rows = maze.length, cols = maze[0].length, queueSize;
        Queue<int[]> queue = new LinkedList<>();
        boolean[][] visited = new boolean[rows][cols];
        int[] curr;
        int[][] dirs = {{0,1},{0,-1},{1,0},{-1,0}};
        int x, y, steps = 0;
        
        queue.offer(entrance);
        visited[entrance[0]][entrance[1]] = true;
        
        while (!queue.isEmpty()) {
            queueSize = queue.size();
            steps++;
            
            for (int i=0;i<queueSize;i++) {
                curr = queue.poll();
                
                for (int[] dir: dirs) {
                    x = dir[0]+curr[0];                    
                    y = dir[1]+curr[1];
                    
                    if (x<0||x>=rows||y<0||y>=cols) continue;
                    if (visited[x][y] || maze[x][y] == '+') continue;
                    
					// check if we have reached boundary
                    if (x==0||x==rows-1||y==0||y==cols-1) return steps;
                    
                    queue.offer(new int[]{x, y});
                    visited[x][y] = true;
                }
            }
        }
        
        return -1;
    }
}