Leet code 1901: – Find a Peak Element II

A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.

Given a 0-indexed m x n matrix mat where no two adjacent cells are equal, find any peak element mat[i][j] and return the length 2 array [i,j]. You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell. You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time.

Flow Diagram: –

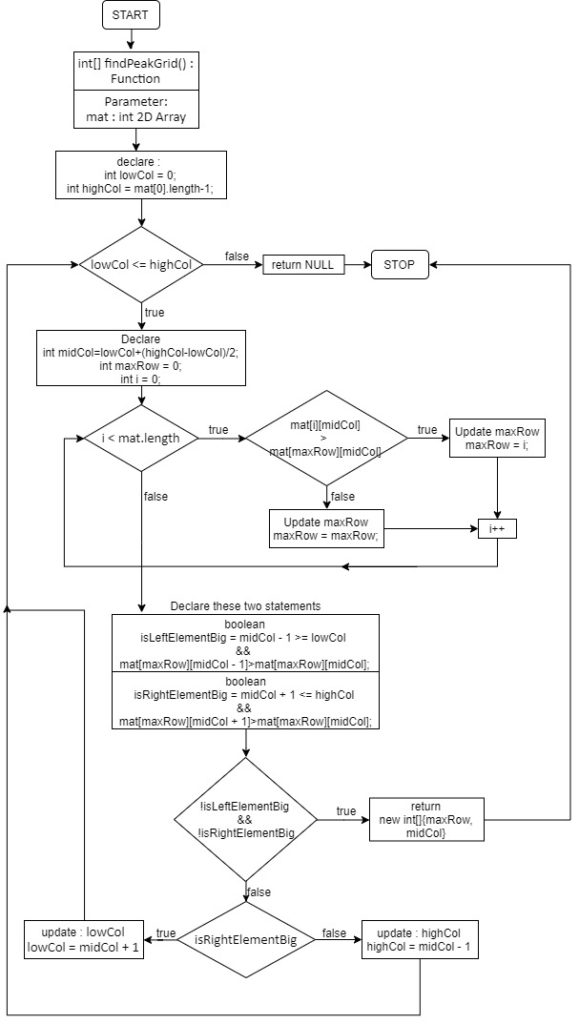
Solution :-

class Solution {
    public int[] findPeakGrid(int[][] mat) {
        
        //Simple explanation:
        // The problem is finding the peak elements of array(maximum element of each column)
        // do binary search for max element column array
        // Time Complexity is M*log(N)
        int lowCol = 0;
        int highCol = mat[0].length - 1;
        
        while(lowCol <= highCol) {
            int midCol = lowCol + (highCol - lowCol) / 2;
            int maxRow = 0;
            for(int i = 0; i < mat.length; i++) {
                maxRow = mat[i][midCol] > mat[maxRow][midCol] ? i : maxRow;
            }
            
            boolean isLeftElementBig = midCol - 1 >= lowCol && mat[maxRow][midCol - 1] > mat[maxRow][midCol];
            boolean isRightElementBig = midCol + 1 <= highCol && mat[maxRow][midCol + 1] > mat[maxRow][midCol];
            
            if(!isLeftElementBig && !isRightElementBig) {
                return new int[]{maxRow, midCol};
            } else if(isRightElementBig) {
                lowCol = midCol + 1;
            } else {
                highCol = midCol - 1;
            }
        }
        return null;
        
    }
}