You are given two strings s and p where p is a subsequence of s. You are also given a distinct 0-indexed integer array removable containing a subset of indices of s (s is also 0-indexed).
You want to choose an integer k (0 <= k <= removable.length) such that, after removing k characters from s using the first k indices in removable, p is still a subsequence of s. More formally, you will mark the character at s[removable[i]] for each 0 <= i < k, then remove all marked characters and check if p is still a subsequence. Return the maximum k you can choose such that p is still a subsequence of s after the removals. A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
Example 1:
Input: s = “abcacb”, p = “ab”, removable = [3,1,0]
Output: 2
Explanation: After removing the characters at indices 3 and 1, “abcacb” becomes “accb”.
“ab” is a subsequence of “accb”.
If we remove the characters at indices 3, 1, and 0, “abcacb” becomes “ccb”, and “ab” is no longer a subsequence.
Hence, the maximum k is 2.
Example 2:
Input: s = “abcbddddd”, p = “abcd”, removable = [3,2,1,4,5,6]
Output: 1
Explanation: After removing the character at index 3, “abcbddddd” becomes “abcddddd”.
“abcd” is a subsequence of “abcddddd”.
Example 3:
Input: s = “abcab”, p = “abc”, removable = [0,1,2,3,4]
Output: 0
Explanation: If you remove the first index in the array removable, “abc” is no longer a subsequence.
Constraints:
1 <= p.length <= s.length <= 105
0 <= removable.length < s.length
0 <= removable[i] < s.length
p is a subsequence of s.
s and p both consist of lowercase English letters.
The elements in removable are distinct.
Flow Diagram: –
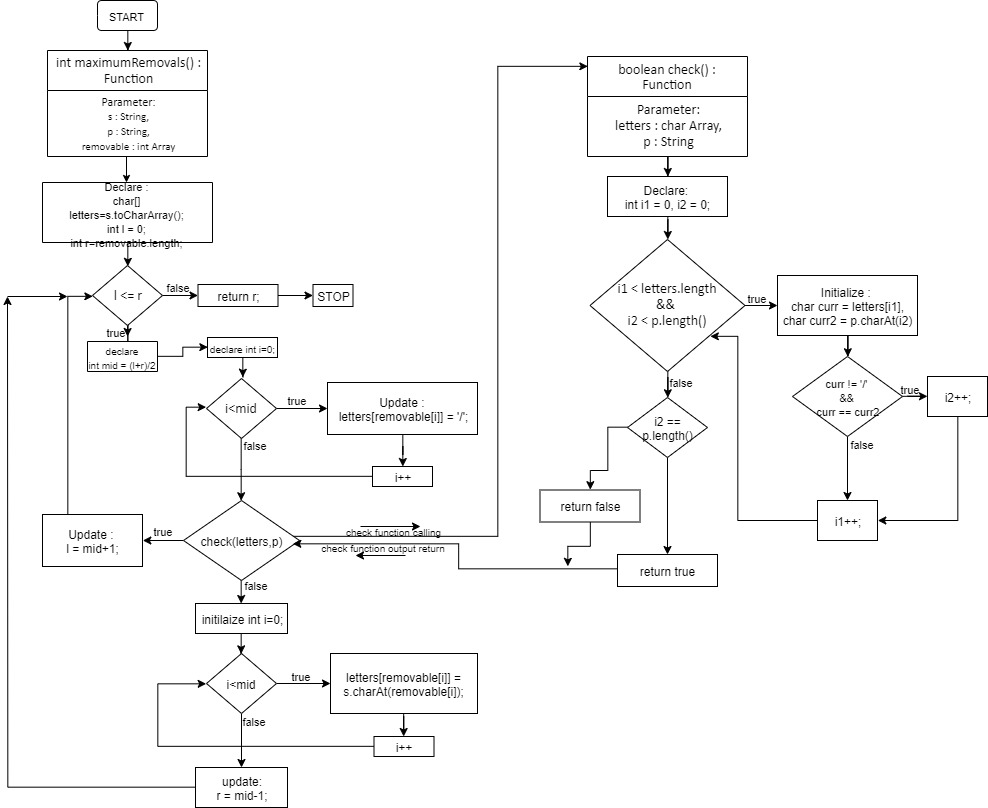
Solution :-
class Solution {
public int maximumRemovals(String s, String p, int[] removable) {
//This question took me 3 wrong attempts before I realized that binary search works the best.
// What do I binary search then? I find the number of elements I can remove!
// The left boundary represents the lower limit (0 at first) while the right boundary represents the upper limit (the length of the removable array)
// Each time, I find the middle number (which is an attempt to remove that number of letters from the string)
// I also use an array of characters and replace those letters removed with the '/' symbol (can choose anything as long as it's a non-letter)
// This should be faster and more convenient to work with as compared to removing letters directly from a string (high time complexity from string concatenation)
//Firstly, I express the letters into an array of characters
char[] letters = s.toCharArray();
//Set up my boundaries.
int l = 0, r = removable.length;
while (l <= r) {
//'mid' represents how many letters I remove this round.
int mid = (l+r)/2;
//'Remove' those letters!
for (int i=0;i<mid;i++) letters[removable[i]] = '/';
//I perform a simple check to see if p is still a subsequence of it. If it is, change the lower boundary.
if (check(letters,p)) l = mid+1;
//Otherwise, I replace back all the letters that I had removed.
//Then, I change the upper boundary.
else {
for (int i=0;i<mid;i++) letters[removable[i]] = s.charAt(removable[i]);
r = mid-1;
}
}
return r;
}
//This is a standard procedure for checking if p is a subsequence of the array of characters.
//I use two-pointers to keep track of which char I'm looking at now in the char array, and another to keep track of which char I'm looking at in p.
// If the character wasn't 'removed' (remember this is indicated by the '/' symbol) and the characters are equal, I increment both pointers.
//Otherwise, I only increment the first pointer pointing to the array of characters.
public boolean check(char[] letters, String p) {
int i1 = 0, i2 = 0;
while (i1 < letters.length && i2 < p.length()) {
char curr = letters[i1], curr2 = p.charAt(i2);
if (curr != '/' && curr == curr2) i2++;
i1++;
}
//If i2 == p.length(), it means that I had managed to match all of the characters in String p!
if (i2 == p.length()) return true;
return false;
}
}