Now imagine an Array where the numbers are stored in an orderly manner. Means minimum index stores the lowest number and the maximum index number (Here the number is 6) stores the highest number but in the orderly manner. Please take a look for a sample ordered Array as shown below:-
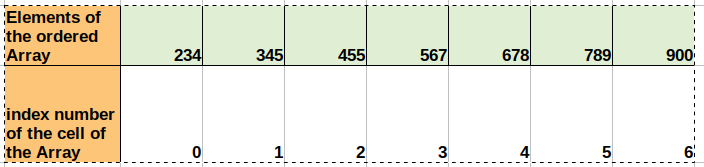
Here in the above picture the numbers are stored orderly from lowest to highest (234 to 900) . Now the main advantage of using the Ordered Array over the unordered Array is the search operation. Here we can use the binary search algorithm over the linear search , which is much faster than the linear search. But in case of unordered Array we can only use the linear search. Now lets talk about the binary search in details.
Power of Binary search in the Ordered Array:-
Binary search is more like the number guessing game that we used to play in our childhood. What should be the approach to find a number that you guessed and which is situated between 1 and 20. The very dumb approach would be check each and every elements of the Array that would be used in case of unordered Array. This is called the Linear Search.
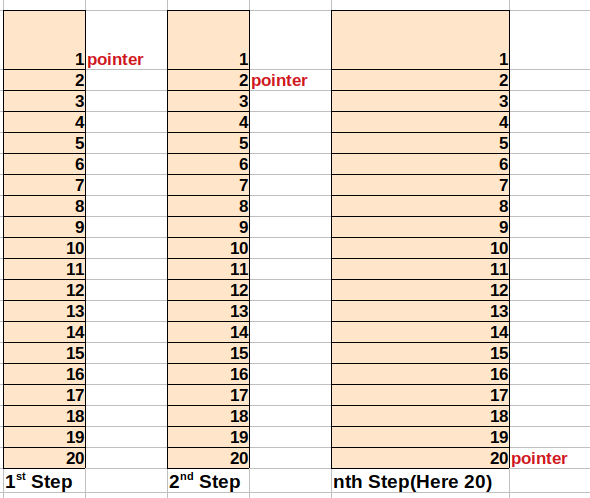
Now here the cost is O(n) as we have to consider always the worst case scenario.
Now in case of Ordered Array we can use another smart approach. Suppose user have guessed 14 and as mentioned the range is 1-20. Now using Binary search this number can easily be found at 4th step.
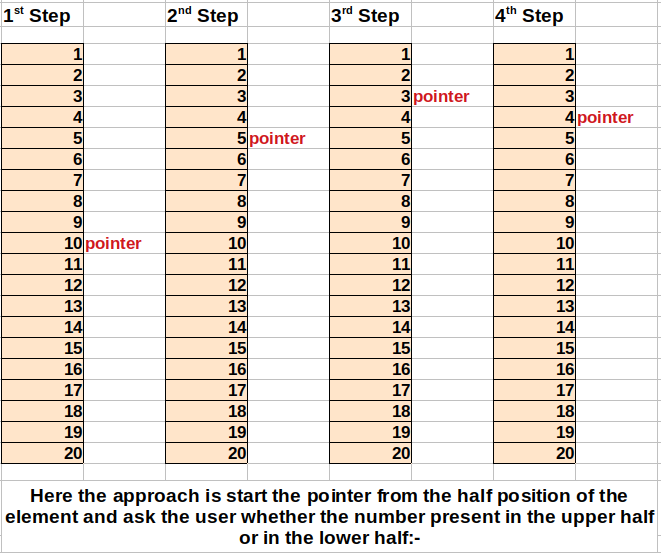
As shown in the above image, the pointer of the binary search algorithm will start from the half position, that is from 10 when the number range is 1-20. Then the pointer will check whether the number that user wants, present in the upper half of the range or in the lower half of the range. In the case of above image, user has guessed 4, that is present in the upper part. So pointer again will divide the number in half, that is, in step 2 the pointer will move to the position where element is 5 because (10/2 = 5), and again will check the element in this position is greater than or less than the number user has guessed. So any number present between 1-20 can be found by using only 4 steps. Now what is the cost of this Binary search?

When the range is 1 to 10, then any number can be found using only 4 steps, and it can be shown that for range 1 to 1000, the number of steps is only 10. And we also know that base 2 logarithm of number 10 is around 4 (3.32) and base 2 logarithm of number 1000 is 9.96 which is almost equal to 10. So, the steps for the binary search can be represented as log2(range). Now in the calculation of Big-O, constant does not matter if the number of steps is very high. So during the representation of the Big-O we can avoid the base of the logarithm and simply can represent it as log(N). Which is much more efficient than the linear search. And the efficiency will increase as we move to higher values of N.