Given an integer k, return the minimum number of Fibonacci numbers whose sum is equal to k. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
F1 = 1
F2 = 1
Fn = Fn-1 + Fn-2 for n > 2.It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to k.
Example 1:
Input: k = 7
Output: 2
Explanation: The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, …
For k = 7 we can use 2 + 5 = 7.
Example 2:
Input: k = 10
Output: 2
Explanation: For k = 10 we can use 2 + 8 = 10.
Example 3:
Input: k = 19
Output: 3
Explanation: For k = 19 we can use 1 + 5 + 13 = 19.
Flow Diagram: –
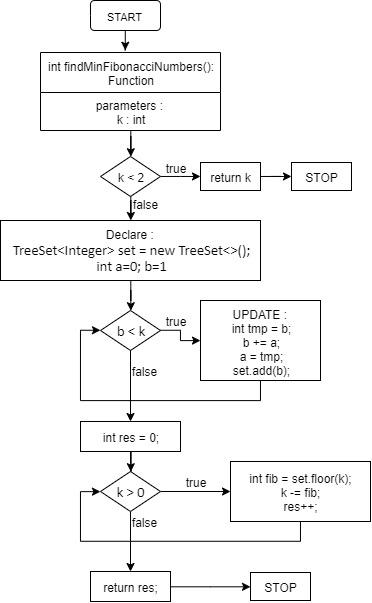
Solution:-
public int findMinFibonacciNumbers(int k) {
if (k < 2) return k;
TreeSet<Integer> set = new TreeSet<>();
for (int a = 0, b = 1; b < k;) {
int tmp = b;
b += a;
a = tmp;
set.add(b);
}
int res = 0;
while (k > 0) {
int fib = set.floor(k);
k -= fib;
res++;
}
return res;
}