Given an expression string exp, write a program to examine whether the pairs and the orders of “{“, “}”, “(“, “)”, “[“, “]” are correct in exp.
Example:
Input: exp = “[()]{}{[()()]()}”
Output: Balanced
Input: exp = “[(])”
Output: Not Balanced Logic:
Given String:-
Step 1:- Take this String as an input of the function. This Function will return the Boolean.

Step 2:
Check all the opening brackets present in the String. And push all the opening brackets in a stack. This search will happen using for loop. So we will start from extreme left position of the given String, and will move one by one to the right side. And all the closing brackets, if any found will be pushed to the stack data structure which will be created.
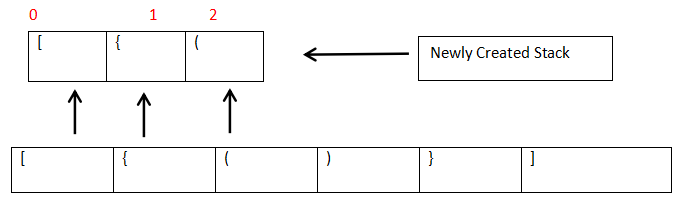
Step 3:-
Check now if the newly created stack, where we have pushed all the opening brackets is still empty or not? If it’s empty, then No opening brackets is present. So there is no need to check further. So we will return false from here.
Step 4:-
Then we will pop it from the newly created stack. Pop will happen in LIFO style as it’s stack Data Structure. As at last, ‘(‘ entered into the stack, So that will be the first one to be popped.
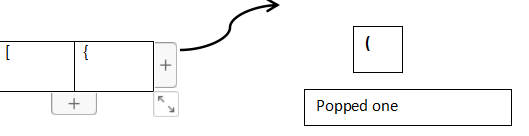
Step 5:-
And then remaining String will be checked, one by one. If the immediate next String is matching with the Popped brackets, then it will be a match and then again will check the next one.
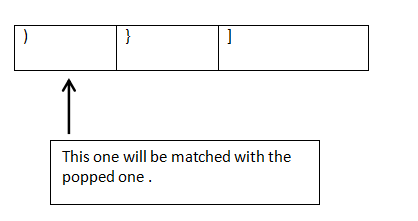
Code:-
import java.util.ArrayDeque;
import java.util.Deque;
public class BalancedBracketCheck {
public static boolean balancedBracketChecking(String expr)
{
//Dequeue used for performance benefit
ArrayDeque<Character> tempStack = new ArrayDeque<>();
int n = expr.length();
for (int i = 0; i < n; i++) {
// check for all the opening brackets
if (expr.charAt(i) == '(' || expr.charAt(i) == '{' || expr.charAt(i) == '[') {
tempStack.push(expr.charAt(i)); // Pushed the opening Bracket
}
// check the stack at this point is empty or not
System.out.println(tempStack.toString());
System.out.println("Count is " + i);
if (tempStack.isEmpty()) {
return false;
}
char tempStore = expr.charAt(i);
switch (tempStore) {
case ')':
// popped the character
char temp = tempStack.pop();
if (temp != '(')
{
return false;
}
break;
case '}':
// popped the character
temp = tempStack.pop();
if (temp != '{')
{
return false;
}
break;
case ']':
temp = tempStack.pop();
if (temp != '[')
{
return false;
}
break;
}// end of switch
} // end 0f for loop
return tempStack.isEmpty();
}
public static void main(String[] args) {
String input = "[{()}]";
int n = input.length();
if (balancedBracketChecking(input)) {
System.out.println("Balanced String");
}
else {
System.out.println("Unbalanced String");
}
}
}
Big(O) Analysis:-
Here Time complexity is :- O(n)
Space complexity is also :- O(n) as here new stack data structure is created. Although Dequeue is used for performance benefit